Tags:
Journalism of Courage
John Nash, the Princeton University mathematician portrayed by Russell Crowe in ‘A Beautiful Mind’, died last weekend. His major contributions came in the field of game theory, and one game he discovered/invented can be a wonderful diversion. It’s called Hex, with rules so simple that a child can play it, yet with strategies that call for extensive analysis.
Hex is not Nash’s exclusive creation, though. The original creator, in 1942, was Piet Hein, a Danish physics student-turned-engineer/inventor. Independently, Nash “re-invented” the game in 1948.
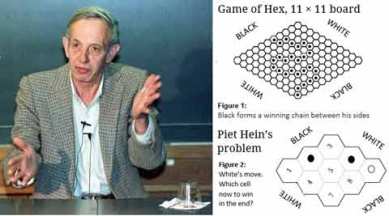
Hex is played on a diamond-shaped board made of hexagons, the number of which can vary (see illustration above). It is between two players, who may be called “Black” and “White” and who are given a number of black and white pieces respectively. Two opposite sides of the diamond are called “black”, the other two called “white”. The four corners belong to either player.
By turn, each player places one piece on any hexagon, as long as that space isn’t already occupied. Black’s objective is to create an unbroken chain of black pieces between the “black” sides; White’s objective is to create an unbroken white chain between the “white” sides. In the illustration, the 11×11 board shows a winning chain for Black.
The game cannot end in a draw; it has been proved that one player will always complete a chain. In fact, Nash proved that if the two players are equally skilled, the player who makes the first move will win. Nash wrote his proof in a cheerful letter to Gardner in 1957, a scanned copy of which is on this website.
In my illustration, the 3×3 board shows a problem posed by Hein. I have numbered his hexagons 1 to 9 for easy identification. Black has taken hexagons 2 and 6, White has taken hexagon 9 and has the next move. Which hexagon should White occupy, asks Hein, to ensure he wins in the end?
Puzzle#12A: Gardner’s book shows us which hexagon White needs but does not give a complete analysis. So I’ve been trying, one step at a time. Once you get down to your own analysis, try and keep updating me with findings.
What you wrote
The Del-Mu-Ka triangle of last week caused a lot of torment to readers, not all of whom managed to solve it.
Dear Kabir, Puzzle#11B — 200 km. Tangents to a circle from a point are equal in length. Hence BR = BP and CR = CQ.
AB + BC + CA = AB + BR + RC + CA = (AB + BP) + (QC + CA) = AP + AQ = 100 + 100 = 200.
Amazing blog!! Kudos!
— Jaysun Antony Alumkal (Coordinator, Academic Committee, IIM Raipur)
Puzzle#12A is best solved with the equation (see illustration) used by Sampath Kumar V (IIM Kozhikode alumnus) and Harsha T R (NIT Karnataka, batch of 2012). Harsha was initially trying a better-known equation:
A = √s(s – a)(s – b)(s – c)
Bindia George (IT engineer, Kochi) and Tushar Gupta (DoMS, IIT Madras) were working with the same equation. It’s a painful process, which gets into higher and higher powers while the √ sign continues to hang around.
Sathya Prakash, who develops software in New Jersey, had no problem; he solved the equation with Oracle.
Biren Parmar (PhD student, Texas A&M University) asked for a hint. I circulated a mail among readers who were updating me about their efforts; I guided them to a web page that has the lesser known equation. Biren solved this equation with a computer program.
Sampath and Harsha wrote to say they had found the equation before my email came. They solved it to get the distance between Mumbai and Delhi as 1,120 km. That’s right; the equation reduces to a quadratic that can be solved with pen, paper and a calculator.
Tushar turned the offer down, saying he had used Excel to solve the better known equation. Sorry, Tushar, but your answer of 1,114 km is wrong. Nitin Saraswat (Bank of America, Gurgaon) took my hint and used Excel on the other equation. He too got it wrong: 1,142 km.
Puzzle#11B was solved correctly by everyone named above.
Another board game
Puzzle#12B: In Scrabble, the letters A, E, I, O, U, L, N, S, T, R count for 1 point each; D, G for 2 each; B, C, M, P for 3 each; F, H, V, W, Y for 4 each; K for 5; J, X for 8 each; Q, Z for 10 each. Spell out a number so that its letter values add up to that number. No premium squares.
Please mail your replies to:
kabir.firaque@expressindia.com
